The first milestone in the development of NUMO was to make sure the equations driving the dynamics of the ocean are solved correctly. The underlying dynamics (i.e. velocity and pressure) in the model are governed by the incompressible Navier-Stokes equation (INSE). You can read more details on the equations and numerical methods that solve them on the Model page.

To validate the implementation of INSE in NUMO, we have used two benchmarks with analytic solutions: Kovasznay flow and Taylor vortex. For the purpose of these tests, we do not include buoyancy and Coriolis source terms.

Kovasznay flow

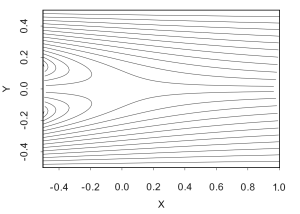
The first solution was provided by Kovasznay [1] in 1948, which represents a steady state laminar flow behind a two-dimensional grid. Here we solve this flow using a full 3D model and expect z component of velocity to vanish. The exact solution is given by:

where

and . The streamlines of the solution look as follows:

We apply Dirichlet boundary condition on velocity using the exact solution and run simulation either from a warm (with initial condition close or equal to the exact solution) or cold start (initially ). Convergence results reported here were obtained using a warm start with the exact solution as an initial condition, however evolving the solution from a cold start to a steady state yields the same results.

Convergence rates

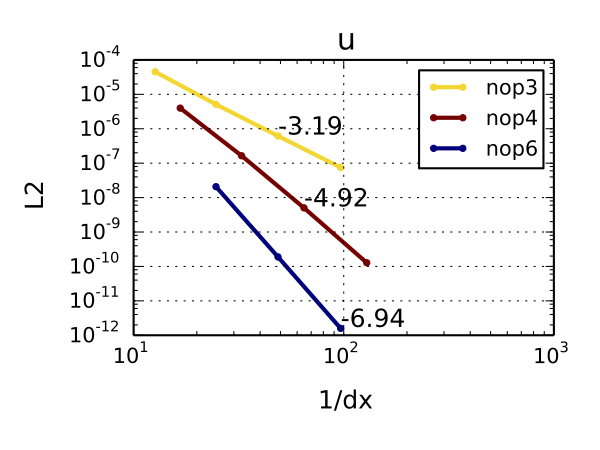
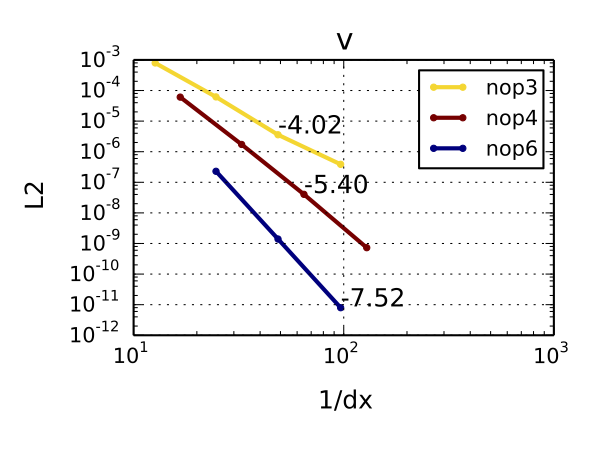
At this stage of development, we use only continuous Galerkin method for its conceptual simplicity. To check for correctness of the implementation of fractional step method (see Model for details) we plot the L2 normalized error of the computed streamwise (u) and spanwise (v) velocity against the inverse of grid resolution (1/dx), first on a structured uniform mesh.

We report the results for three polynomial order expansions (nop=3, 4, 6) which define the convergence order of the method. Theoretically, we expect the convergence rates to be nop+1. The numbers above the plot lines correspond to convergence rates calculated from simulation results.  The computed convergence rates match the theoretical ones, with v velocity rates being consistently higher than streamwise velocity convergence. We do not present the w velocity results (perpendicular to u,v plane) since there is no convergence in that direction as the values of this velocity component oscillate around machine zero.

Unstructured mesh convergence

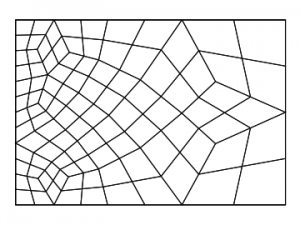
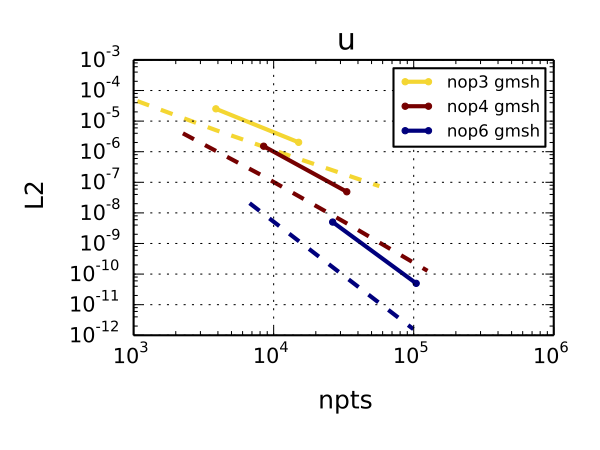
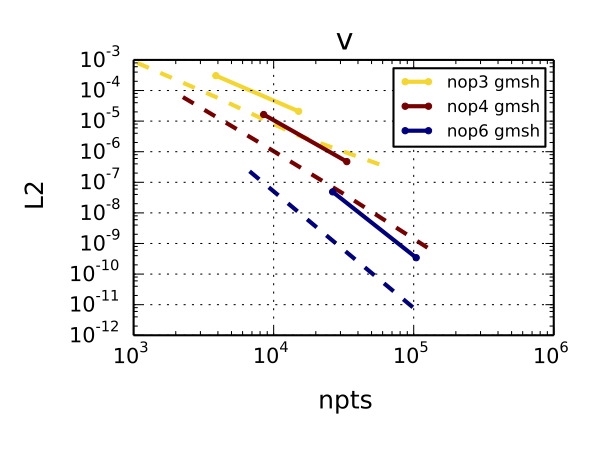
To verify unstructured mesh capability we have performed the same test on a series of grids generated by gmsh. Here we present only one such grid for illustration purposes.

This time a direct computation of a representative grid resolution was not possible, so we are plotting L2 errors against the number of points in the x-y plane. We intentionally do not include points in the z direction, as increasing the resolution in that direction does not contribute to an improved solution of this 2D problem. As a comparison, we plot in dashed line the results of structured mesh simulations rescaled using the same metric.

The convergence slope for all polynomial orders is similar to the reference structured grid simulation (dashed line) for both u and v velocity, which means that the unstructured grid does not hurt the convergence rates. It is causing a shift upward in the error norm plot, but this is expected behavior as the flow is not as well aligned with the grid as for the structured mesh.

Taylor vortex

The Kovasznay flow test was checking for spatial convergence properties of the model, so effectively it was testing the CG method implementation in NUMO. The task of the Taylor vortex [2] is to check the time convergence rates, as this is an unsteady flow. This is a benchmark for the implementation of the stiffly-stable time integration method (see Model for details). The domain is a square defined by the coordinates in each direction. Again, we solve this 2D problem in 3D. The exact solution is:

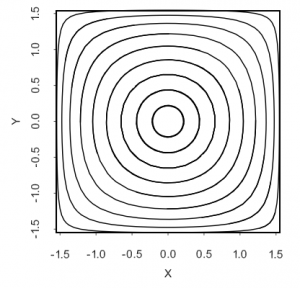
and we choose . The boundary conditions are again Dirichlet using the exact solution at the boundary. The image below shows the Taylor vortex streamlines at the initial time. We run the simulation for one full revolution of the flow, i.e. until .

Time convergence rates

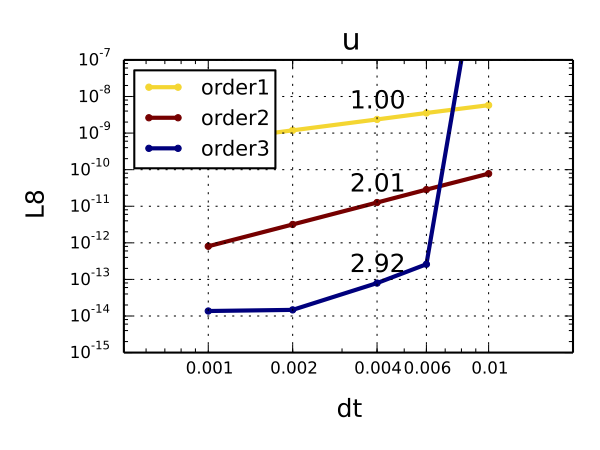
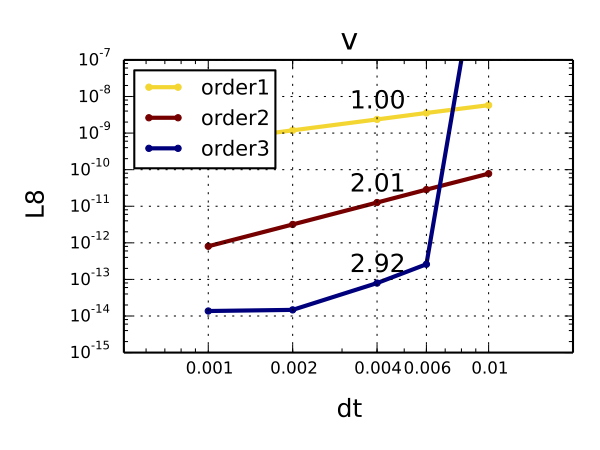
This time we plot the L-infinity norm (L8, a.k.a. maximum norm) against the time-step size for three different orders of time convergence (the stiffly-stable method is, in fact, a suite of backward-difference methods up to 3rd order).

All methods show convergence rates matching the theory very well. The 3rd order method for small time-steps hits the machine precision accuracy and tails off, which is an expected behavior. For larger time-steps, it becomes unstable, but if we increased the time-step further the method would get stable again, which is the property of a 3rd order backward difference method. This test confirms that we can safely use time integration up to 2nd order.

Summary

We have tested the implementation of space and time discretization schemes in NUMO. Both Kovasznay flow and Taylor vortex test cases give very satisfactory results. The unstructured mesh does not hurt the convergence rate of continuous Galerkin method, and we expect the same result from discontinuous Galerkin method. Time integration schemes behave as expected up to 2nd order. Third order scheme becomes unstable for some time-steps. For that reason, the second order method will be the time integrator of choice.

---

[1] Kovasznay, L. I. G. “Laminar flow behind a two-dimensional grid.” Mathematical Proceedings of the Cambridge Philosophical Society. Vol. 44. No. 01. Cambridge University Press, 1948.
[2] Karniadakis, G., and Spencer S. “Spectral/hp element methods for computational fluid dynamics.” Oxford University Press, 2013.